数学の問題を出すのは久しぶりのような感じがするKWC企画世話人です。
今回の問題は2010年の数学オリンピックの予選の問題です。
【問題】
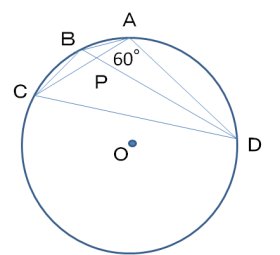
四角形ABCDは半径1の円に内接し、対角線同士のなす角は60度である。対角線の交点をPとすると、AP=1/3、CP=2/3である。このときBPとDPの差の絶対値としてありうるものを全て求めよ。
数学オリンピックの時には、上の図が付いていないようなのですが、特別にわたしが描いた下手な図をつけることにしました。参考にしてください。
数学オリンピックは高校生が対象かと思いますが、この問題は、中学生の知識で十分に解けます。
楽しんでください。
わたしは、寝る前に1杯飲んだだけでは答えが思いつかず、翌朝の通勤時間にようやく答を思いつくという情けない状態でした。
#その他
