図形の問題は発想も大事だと改めて認識したKWC企画世話人です。
ウイスキーで酔っ払ってやるのに、ちょうどいい問題だったかも(笑)
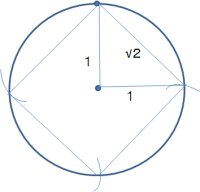
まず、できあがりのイメージを作ります。
すると一番上の図のように、半径1の円の場合には、円周を四等分するには、長さ√2を作り出さなければならないことがわかります。難しそうですが、作り出すべき長さがわかったわけです。
ターゲットは√2を創りだすことです。
では、順番にやっていきます。2番目の図をみてください。
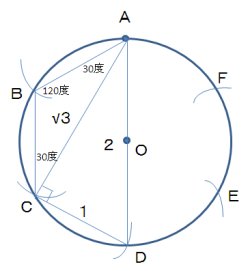
半径1と同じ長さで円周を区切っていくと、ちょうど六等分できることがわかります。これは内接する正六角形を考えていただければすぐにわかるはずです。
今、この図から得られる長さを全て書き出してみます。本当は定規を使えないので、線分はないのですが、分かりやすくするためです。
三角形ACDは直角三角形で各辺の長さが1:2:√3になるとわかります。これが、いまわかる全ての線分の長さ。これから√2を創りだすのです。
3番目の図に移ります。
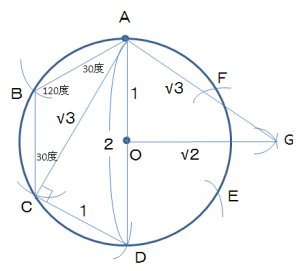
コンパスを√3の長さであるACに合わせて点Aと点Dから円弧を書いて交点Gを書きます。すると、三角形AOGは√3と1の長さを持つ直角三角形になっていますから、OGは√2とわかり、うまく作り出せました。
あとは、点Aと点Dから√2に合わせたコンパスで円周に印をつけるだけ!
コンパスだけでやったイメージの図を一番したに付けました。
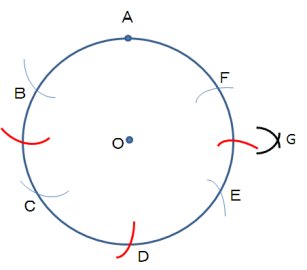
いかがでしたでしょうか?
この図形問題を考えながら飲むといつもより3倍飲めるとおっしゃってくださった方がございましたので、出題した側としては本望でございます。
#その他
