円高の話ではありません(笑)。円の面白い性質を見つけたKWC企画世話人です。
半径1の円(これを単位円といいます)に円周をn等分する点をn個おきます。一つ点を選んで、この点と他の点を結ぶと(n-1)本の線分ができます。これらの長さを掛け算していくと答えがnとなるというものです。
まず、やってみましょう。
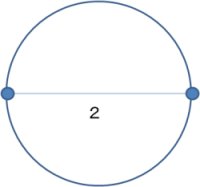
n=1はないので、n=2の場合から。これは上の図を参照してください。
n=2では、円周を2等分する訳ですから、2点を結ぶ線分1本しかできませんし、これは直径にほかなりません。今半径が1ですから、直径は2となってn=2です。
n=2のときは成立ですね。
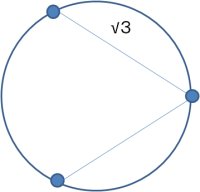
n=3の場合
これは、内接する正三角形ができるように点をおきます。線分は正三角形の辺の長さに相当するものが2本できます。一辺の長さは√3になりますから、√3x√3=3となって、これまた成立します。
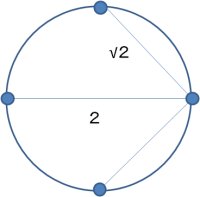
n=4の場合
これは、内接する正方形ができるように点をおけばOKです。線分は、正方形の辺の長さに相当するものが2本と直径に等しいものが1本できますから、求める掛け算は
√2x√2x2=4
となって、これまた成立します。
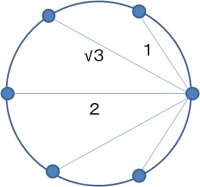
n=5は面倒なので、ちょっとパスしてn=6をやります。
今度は内接する六角形です。できる線分は、1が2本、√3が2本、2が1本です。つまり、
1x1x√3x√3x2=6
やはり成立してしまいます。
n=5やn=7のときに実際に成立するかどうか確かめられますか?
それとこれを一般的に証明できる強者はいらっしゃいますか?
