今日はとある大学の大学院生にヒトコマ講義しなければならないKWC企画世話人です。
ウイスキーの講義をするわけではありません(笑)。
ということで、みなさんも学校の勉強に戻ってみましょう。
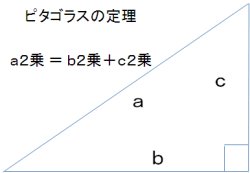
みなさんもピタゴラスの定理をご存知ですよね?
直角三角形の三平方の定理です。中学校のときに、その証明方法を習ったはずですよね。でも、その証明方法は100通り以上あるのだそうです。わたしも驚きました。
わたしが自分でできるうちの5通りを下の方に書いておきます。
(実は、わたしの実力では、あと数通りしかできませんでした。)
それ以外の証明方法を考えてみてください。
何しろあと95通り以上あるはずですから、ウイスキーを飲みながらゆっくり考えてください(笑)。
以下に5通り分を書いておきます。
No.1
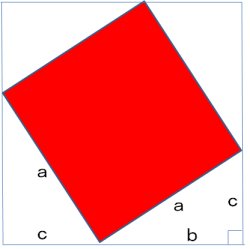
大きな正方形の面積 = 4つの直角三角形の面積+ 赤い正方形
(b+c)x(b+c)=4x1/2 x b x c + a2乗
b2乗+c2乗+2x b x c =2 x b x c + a2乗
a2乗 = b2乗+c2乗
No.2
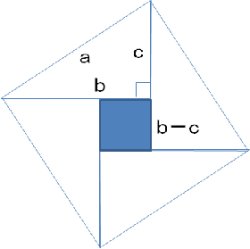
大きな正方形の面積 = 4つの直角三角形の面積 + 青い正方形
a2乗 = (b - c)x(b - c) + 4 x 1/2 x b x c
a2乗 = b2乗+c2乗 - 2x b x c +2 x b x c
a2乗 = b2乗+c2乗
No.3
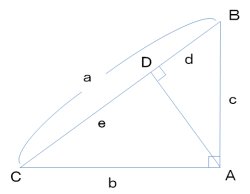
直角三角形の相似をつかう
頂点Aから辺BCに垂線をひく
直角三角形ABCとDBAとDACはお互いに相似ということから
a : c = c : d → ad=c2乗
a : b = b : e → ae=b2乗
両辺たして ad+ae=b2乗+c2乗
a(d+e)=b2乗+c2乗
a=d+e なので
a2乗=b2乗+c2乗
No.4
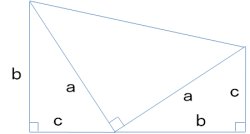
大きな台形の面積=三角形3つの面積の足し算
(b+c)x(b+c)x1/2=2x1/2x b x c + 1/2 x a x a
両辺に2をかけて
b2乗+2bc+c2乗=2bc+a2乗
なので
a2乗=b2乗+c2乗
No.5
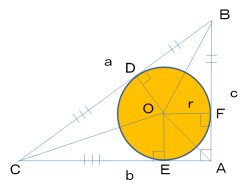
内接する半径 r の円Oを考える
直角三角形ABCの面積=三角形OBC+三角形OCA+三角形CAB
1/2x(bxc)=1/2 x a x r + 1/2 x b x r + 1/2 x c x r
b x c = r x (a+b+c) → r = b x c/(a+b+c)
三角形ODCと三角形OCEが合同なのと
三角形OBDと三角形OBFが合同なので
a = ( b - r ) + ( c - r ) = b + c - 2 x r
なので、 r = 1/2 x ( b + c - a)
1/2 x ( b + c - a) = b x c/(a+b+c)
これを解いて a2乗=b2乗+c2乗
これで5通りです。
#その他
