パンのように見える不思議な物体が人気で驚いているKWC企画世話人です。
ところで、昨日の図形問題は楽しんでいただけたでしょうか?
半径2の円に半径3の円を接するようにおいて、大きな円が重ならいように置くときに、最大何個までおけるか?という問題でした。
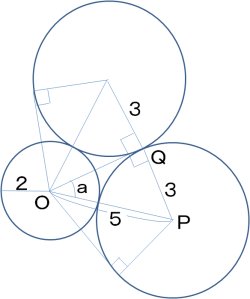
では解答です。上の図を見てください。
二つの円が接するところで、お互いの円の中心を結び線を引きます。この線分の長さは5になります。半径2の円の中心Oから半径3の円に接線を引いて、その接点Qと半径3の円の中心Pを結びます。すると三角形OPQは、直角三角形で斜辺の長さが5で、もう一つの辺の長さが3ですから、あと一つの辺の長さも4とわかります。
角POQをaと表すことにすると、n個の大きな円を置くと
nx2xa ≦ 360度
a ≦ 180度/n
という関係が成立するだけ、大きな円が置けることになります。
sin(a)=3/5=0.6
ということは分かっても、角度aはすぐにはわかりそうにありません。
なので、sin(a)と sin(180度/n)の値を比べていくことにします。
大きな円は3個は確実におけますから、それより大きいところを見ていきましょう。
4個の場合を考えましょう。n=4です。
sin(180度/4)
=sin(45度)
=1/√2=√2/2
≒1.414/2
≒0.707
√2はヒトヨヒトヨニヒトミゴロでしたね(笑)。
0.6=sin(a)<sin(180度/4)≒0.707となって、4個がおけることが数式の上からも確かめられたわけです。
では、5個はおけるか?
n=5
sin(180度/5)
=sin(36度)
あれ、いつぞや出てきましたね~(笑)。そうです。正五角形のときにでてきました。
sin(36度)={√(10-2√5)}/4
という2重根号のややこしいやつでした。
とりあえず、ニ乗してみましょう。二重根号がはずせますから。
sin(36度)のニ乗=(10-2√5)/16
≒(10-2x2.236)/16
≒0.3455
√5は、フジサンロクオームナクです(笑)。
sin(a)=0.6 ですから
sin(a)のニ乗=0.36
ということで、
sin(a)のニ乗 > sin(180度/5)のニ乗
となってしまいました。ということは、両者とも正の数ですから、
sin(a)> sin(180度/5)
ということになって、大きな円5個は置けないということがわかります。
ちなみに6個は sin(30度)=0.5<0.6=sin(a) ですから、置けないことがすぐにわかります。
答えは、半径3の円は4個まで接するようにおけるということになります。
でも、sin(a)のニ乗とsin(36度)のニ乗の差がとても小さいので、いい加減な作図をすると5個でも置けちゃうと作図する場合があるかもしれません。注意が必要です。
この解き方は、sin(36度)が必要なので、高校生の数学を学んでいないと解けないわけです。
いつもよりたくさん飲めた方々がいらっしゃることを祈っております。
#その他
