
昨日の記事は沢山アクセスがあってちと緊張しているKWC企画世話人です。
図形の問題の解答です。この問題は1962年の東大入試にもでたことがある問題なのですが、よ〜く考えると中学で習うことだけで解けるという問題だったりします。
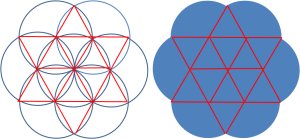
2番目の図をみてください。
実は、7つの円がつくる交点をこの図のように結んでみると意外に簡単そうだと気が付きます。
左側の図は相変わらず煩雑なので、右側をみてください。
こうやって見ると、全て同じ扇形6個と全て同じ三角形12個を足し合わせるだけで、この面積が過不足なく計算できることになります。
では、扇形の面積は、半径Rが分かっていますから、あとは中心角だけわかればOKですね。
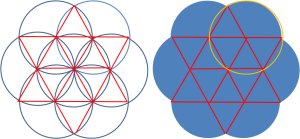
三番目の図に移ります。
黄色の円に注目すると、中心角は360度から4つの正三角形の角を引き算すればよいことがすぐにわかるので、120度ということがわかります。残りの扇形も一緒です。確かめてみてください。
ということで、一つの扇形の面積は、円周率をPIと置いて、
PIxRxRx(120/360)
=PIxRxRx(1/3)
となります。
次は三角形です。これもよ〜く見ると、辺の長さが全て半径Rに等しいことがわかりますから、一辺の長さがRの正三角形の面積が分かればよいことになります。
(1/2)xRx{(√3/2)xR}
=(√3/4)xRxR
あとは、掛け算と足し算です。
6個の扇形の面積 + 12個の正三角形の面積
=6xPIxRxRx(1/3)+12x(√3/4)xRxR
=2xPIxRxR + 3√3xRxR
=(2xPI+3√3)xRxR
めでたし、めでたし。
もう一つ、別の解き方があります。
次の図を見てください。
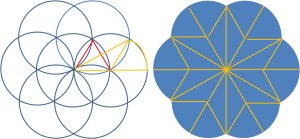
左側の図に注目してみると、黄色の線で囲まれた図形の面積の12倍の面積が青色の部分と同じ面積とわかります。
黄色の扇形の部分は、60度の扇形なので
PIxRxRx(60/360)
=PIxRxRx(1/6)
黄色の三角形の部分は、底辺がR、高さが(√3/2)xRなので
(赤の正三角形と同じ面積とわかります)
(1/2)xRx{(√3/2)xR}
=(√3/4)xRxR
12x{PIxRxRx(1/6)+(√3/4)xRxR }
=2xPIxRxR + 3√3xRxR
=(2xPI+3√3)xRxR
当たり前ですが、同じ答えになります。
なんでこっちの図形を思いついたかというとこの図の方が綺麗だと感じたから(笑)。
右側の図はきれいでしょ?
さて、この問題を考えることで沢山飲めたでしょうか?
#その他
