昨日から帰省して実家でのんびりしているKWC企画世話人です。
では、昨日の問題の解答です。扇形の面積を求め方が必要になります。
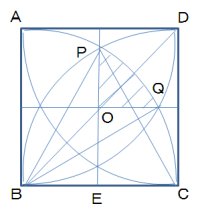
まず、2番目の図のように点に名前をつけることにします。
扇形PBQの面積から三角形PBOと三角形QBOの面積を引き算するという作戦にでます。
必要なのは、角PBQの大きさと三角形PBOの底辺の長さPOです。高さは1/2Rになるから。
与えられた条件を整理します。
ABCDは一辺の長さがRの正方形。
図中の円弧の半径もR。
三角形PBCに注目してください。
点Pは円弧AC上にありますからPA=R
また点Pは円弧BC上でもありますからPC=R
もちろんBC=Rですから、三角形PBCは正三角形です。
すると角PBC=60度です。
また、角DBC=45度なので、
角PBO=角PBC-角DBC=60度-45度=15度
同様に、角QBO=15度
それ故、角PBQ=角PBO+角QBO=30度
これで扇形PBQの面積がわかります。
扇形PBQの面積 = 円周率xRxRx30度/360度
= PIx(Rの2乗)/12
となります。ギリシア文字が化ける可能性があるので、円周率のパイはPIと書くことにします。
次に三角形PBOの底辺POの長さを求めます。
PO=PE-OE ですね。
OE=R/2とすぐにわかります。
PEは、角PCEが60度の三角形PCEの性質から求められます。
PE=Rx√3/2
つまり、PO=Rx(√3 - 1)/2
三角形PBOの面積=(1/2)x(R/2)xRx(√3 - 1)/2
=(Rの2乗)x(√3 - 1)/8
求める面積=扇形PBQの面積 -(三角形PBOの面積の2倍)
= PIx(Rの2乗)/12
-2x(Rの2乗)x(√3 - 1)/8
=(PI + 3 - 3√3)x(Rの2乗)/12
となります。めでたしめでたし。
さて、今日は朝から父と日本酒とウイスキーをしこたま飲む予定です(笑)。
#その他
