数学者のガウスは偉大だったことをしみじみと感じているKWC企画世話人です。
みなさんのまわりには、正五角形を描ける天才小中学生がいましたか?わたしの周囲には残念ながらいませんでした。
まず、正五角形を書く前に、その性質をみる必要があります。
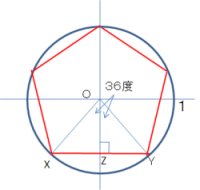
一番上の図をみてみましょう。単位円(半径1の円)に内接する正五角形があったとします
ZY=OY x sin(36度)=sin(36度) で、sin(36度)の値が必要となります。
36度 x 5 = 180度を思いついた方は、sin(2×36度) = sin(180度-2×36度) = sin(3×36度) という関係が得られて、他ごちゃごちゃと三角関数の倍角の公式と3倍角の公式を使って、sin(36度) = √(10 – 2√5)/4 と解くことができて、XY = √(10 – 2√5)/2 が得られます。
つまり、単位円に内接する正五角形の一辺は √(10 – 2√5)/2 となります。
面倒を一つなくすために、単位円ではなく、半径2の円を考えることにすれば、正五角形の一辺の長さは √(10 – 2√5) ということがわかります。
とても面倒そうに見えますが、√5をどっかで作り出せばなんとかなると考えます。
では、正五角形を書くことにします。
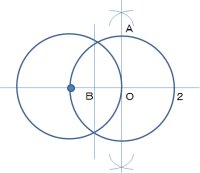
2番目の図をみてください。
直交座標をコンパスで準備して、円をひとつ書きます。半径は2とします。
次に、元の円とX軸の交点(青の点)を中心に同じ半径の円を書きます。元の円との交点が二つできて、この2点を結ぶ線とX軸との交点をBとします。この交点は、半径の半分の長さですから、OB=1となります。
AB = √(OBの2乗 + OAの2乗)
= √(1+4) = √5
AB=√5 となって √5 を創りだしたことがわかります。
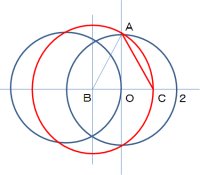
3番目の図に移ります。
点Bを中心にABの長さを半径、つまり半径√5 の円を描きます(赤で示してあります)。この円とX軸との交点をCとします
OC = BC – OB = AB – OB = √5 – 1
AC = √(OAの2乗 + OCの2乗)
= √{(2の2乗) + (√5 – 1)の2乗}
= √{ 4 + 5 – 2√5 +1}
= √(10 – 2√5 )
ということで AC は求める正五角形の一辺の長さと同じだったとわかったわけです。
おまけ、 差はごく小さいのですが AC > AB です。
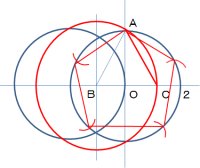
あとは、ACの長さをコンパスで測って、点Aから元の円の円周を等分して、各点を結べばよいわけです。
四番目の図にそれを示しました。
ガウスはこれを正17角形でやってみせたのです。やはり偉大でした。
これで今晩のお酒が美味しく飲めますか~?
#その他
