初等幾何学の問題を携帯でも読めるように書くのは結構面倒だということをやっと理解したKWC企画世話人です。
さっそく、昨日の解答です。
まず問題の確認です。
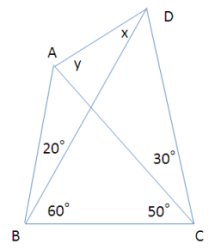
図のような四角形があって対角線が引いてあります。
その角度は図のように与えられています。
そのときの角xおよび角yの大きさを求めよ
一番上の図をみてみましょう。
まず、三角形ABCに注目して、角BACを計算すると50度となることがわかり、角BAC=角ACBとなって、三角形ABCは二等辺三角形となることがわかり、AB=BCとなります。
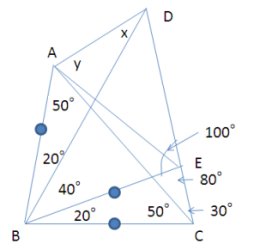
次に2番目の図を見ます。
さらに、BC=BEとなるような点Eをコンパスで決めて、点Aからと点Bから補助線を引きます。
するとBC=BEとなるように引いたのですから、三角形BECは二等辺三角形なので、角BEC=80度、角EBC=20度となります。ついで角DEB=100度となることもわかります。
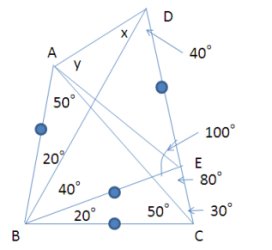
3番目の図をみてみましょう。
三角形BEDに注目します。角DBE=40度、角DEB=100度ですから、角BDE=40度となって、三角形BEDも二等辺三角形であることがわかって、BE=EDということがわかります。
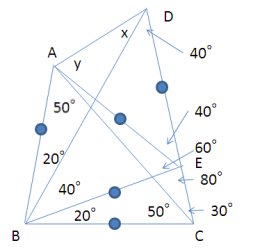
4番目の図に移ります。
三角形ABEに注目します。一番上の図でAB=BCでしたし、BC=BEとなるように点Eを決めたのですから、AB=BEは当然です。さらに、角ABE=80度-20度=60度ということもすぐにわかります。つまり三角形ABEは頂角60度の二等辺三角形つまり正三角形ということが導けるわけです。
ここからAB=BE=AEがすぐにわかります。また角AEB=60度です。
3番目の図でBE=EDとなっていましたから、ED=AEとなります。
そうすると三角形AEDも二等辺三角形ということになります。
角AED=100度-60度=40度なので、角EDA=角EAD=70度となります。
つまり角x=角BDA=70度-40度=30度となります。
また角y=角CAD=180度-角ACD-角CDA=180度-30度-70度=80度
めでたし。めでたし。簡単に見えても難しいでしょ?
今夜はゆっくり一杯やりましょう。
#徒然日記
